Antes de continuar a falar sobre as leis de Newton precisamos falar sobre algo que usamos muito na dinâmica: vetores. Vetores estão presentes em vários lugares, como em jogos, tela de touch e ao exemplificar as forças atuantes em um corpo. O que são vetores?
Os vetores são segmentos de retas que vão do ponto A ao ponto B. Eles têm direção (horizontal ou vertical), sentido(direita ou esquerda) e intensidade (tamanho/módulo).
Vamos observar os vetores abaixo. No primeiro caso o primeiro tem direção horizontal e sentido para direita (positivo). O segundo tem direção vertical e sentido (cima) positivo.
Considerando os sistema de orientação

Figura 1- Orientação de vetores (Rodinei Pachani)
Agora podemos falar um pouco sobre a intensidade do vetor. Ela seria o tamanho da seta, ou do vetor, esta representação pode ser numérica ou por meio da figura apresentada acima.
Usamos muito vetores na física para indicar as forças sendo exercidas em um corpo. Como falei no texto anterior sobre a inércia. Neste texto mostra que normalmente temos várias forças agindo sobre um corpo. Então como podemos dizer qual delas é a maior ? ou qual o valor das soma das forças? E como podemos realizar operações matemáticas com os vetores, sabendo que eles têm direção, sentindo e intensidade?
Vamos pensar que os vetores estão em um gráfico cartesiano. Vamos nomear os eixos, o eixo horizontal o eixo do cosseno com valores da direita positivo e para esquerda negativo. O eixo vertical será o eixo dos senos com orientação para cima positivo e para baixo negativo
Agora um vetor sai da origem do gráfico e anda duas unidades, ou dois quadradinhos para a direita no eixo do cosseno. Podemos dizer então que este vetor tem direção horizontal, sentido positivo e intensidade igual a 2. O mesmo podemos fazer para o vetor que sai da origem e vai para o sentido positivo no eixo do seno andando duas unidades. Este vetor tem direção vertical sentido positivo e intensidade igual a 2. A diferença dos dois vetores é que um vai para direção do eixo cosseno e o outro para direção do eixo seno.
Quando falamos em um plano cartesiano de duas dimensões a letra usada para indicar o eixo x, eixo do cosseno, é a letra e i. E a letra indicada para o eixo y, eixo do seno, é a letra j. Quando usamos o plano cartesiano de três dimensões usamos o eixo z, e a letra indicada para falar do vetor no eixo z é a letra k. A = 2i ; B= 2j ; AB= (2i,2j)

Figura 2 – Vetores em plano cartesiano
Então para demonstrar como como realizamos operações matemáticas com os vetores, vamos falar primeiramente de suas propriedades.
Podemos multiplicar um número escalar (3 e -3)por um vetor o resultado será um vetor com a mesma direção porém em com o sentido a depender do valor do número escalar, se o número for positivo o sentido será positivo, mas se o número for negativo o sentido será negativo.
Vamos pegar o exemplo dos vetores acima A e B se multiplicar o escalar 3 pelo vetor A e o escalar -3 pelo vetor B temos:
3.A = 3. (2i) = 6i ( 6 intensidade/módulo ; direção i = eixo x e sentido positivo).
-3.B = -3 .( 2j) = -6j ( 6 intensidade/módulo ; direção j = eixo y e sentido negativo).
Lembrando que o módulo de um número é apenas o valor numérico sem levar em conta o sinal do mesmo.
Para se fazer a adição e subtração de vetores podemos usar a regra do polígono ou a regra do paralelogramo.
Vamos determinar dois vetores e , sendo horizontal e positivo e diagonal e positivo. Assim vamos somar os vetores desenhando um paralelogramo.


figura 3: Exemplos de prolongamento dos vetores formando um paralelogramo – (Gil da Costa Marques 2007)
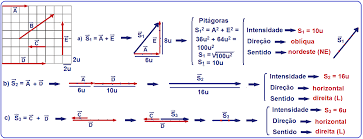
A soma dos vetores e portanto a vetor resultante é dado pelo vetor em vermelho. A partir do paralelogramo identificamos um triângulo e para resolver esta operação usamos a lei dos cossenos. O vetor resultante será diagonal e sentido positivo. S2 = a2 + b2 +2.a.b.cos
v2 = v12 + v22 + 2v1v2cos ,
Agora vamos usar a regra do polígono

figura 4: Exemplo vetores formando um polígono
Tendo os vetores A e B a soma deles resultará no vetor vermelho, para realizar a soma usamos o teorema de pitágoras
a2= b2+c2 figura 4: Exemplo vetores formando um polígono
A subtração é realizada de forma análogo aos passos que realizamos.
Voltando a um vetor em um gráfico cartesiano, agora partindo de qualquer ponto. Analisando segundo as componentes x e y.
Como podemos saber o valor do vetor em relação aos eixos?
Traçamos retas paralelas ao eixo x e ao eixo y no começo (Vx1;V y1) e no final (V x2 ; V y2)do vetor, assim iremos descobrir os valores equivalentes em x e y. Para saber os valores exatos utilizamos a fórmula.
vx = v.cos para x e vy = v.sen para y
Para realizar a soma e subtração neste caso, é necessário levar em conta os valores encontrados no eixo x e y. O Vetor resultante então será o resultado da soma/ subtração das componentes em x e y.
vx = v1x + v2x ,
vy = v1y + v2y .
ou
vx = v1x – v2x ,
vy = v1y – v2y
Para verificar o módulo (ou valor numérico) do vetor, calculamos a raiz quadrada das somas quadráticas das componentes
Fazer uma explicação e análise de vetores antes de continuarmos com os nossos textos sobre as leis de newton se faz necessário porque no próximo texto iremos tratar das forças atuantes em um corpo.
Referência
http://efisica.if.usp.br/mecanica/universitario/vetores/vetores/
https://www.stoodi.com.br/resumos/fisica/vetores/
https://www.sofisica.com.br/conteudos/Mecanica/Cinematica/Vetores.php
Imagem destacada
Vetores – Diferenças entre grandezas escalares e grandezas vetoriais










